So let’s get real about classifying things for a second. When you decide to create some kind of machine learning model (even something as simple as logistic regression or a decision tree), you need some kind of metric to decide if your shiny new classifier is, well, classifying stuff. There’s plenty to consider, especially data issues like imbalanced classes. If you start googling around, you will often find advice about using an “AUC Score”, “AUC”, “ROC”, or some strange combination, especially if your classes are unbalanced.
So you look google those terms, look at your favorite machine learning and data science web sites, do a little digging, and… (If you’re like me) You end up more confused. I admit, while most metrics make intuitive sense, I always found the whole AUC/ROC thing confusing. I think I went back to the standard descriptions and text tons of times over a couple of years before it started to sink in.
Go ahead and read the Wikipedia article on the Receiver Operating Characteristic. I’ll wait. Good, all done? Totally clear? Actually, the last time I checked it was a pretty good article if you already knew what it was talking about and needed a quick brush up on the topic. But if you’re still reading, you’re probably trying to figure out what in the world it means.
Let’s start with some terms we’ll use below. Let’s assume that you’ve got some stuff (or rather, data about some stuff) that you want to classify. For each instance in your data set, you want to apply one of two labels: GOOD and BAD. These aren’t random labels; you’ll see paired terms like positive/negative in the literature. It’s handy to think in terms that you’ll see in the literature, where disease detection and similar tasks are discussed in terms of good/bad. But remember that these label are no more than useful abstractions. If you’re attempting to differentiate between Star Wars and Star Trek, you aren’t building anything that can claim one is inherently better than the other (although we all know that ONE of those is better, amirite?).
An instance with the label GOOD is a “positive” instance. If your classifier correctly labels it GOOD, that’s a True Positive. If you label it BAD, that’s a false negative. Like traditional 2x2 confusion matrix you’ll see everyone write out at some point (there’s even an example at the Wikipedia ROC page). Quick pro tip: terminology for that 2x2 matrix changes across field – so if you see someone refer to Sensitivity and someone else use Recall, don’t freak out. Personally, I always re-google the terms since I can’t keep them all straight 😉
So let’s look at the helpful image we’ve got here.
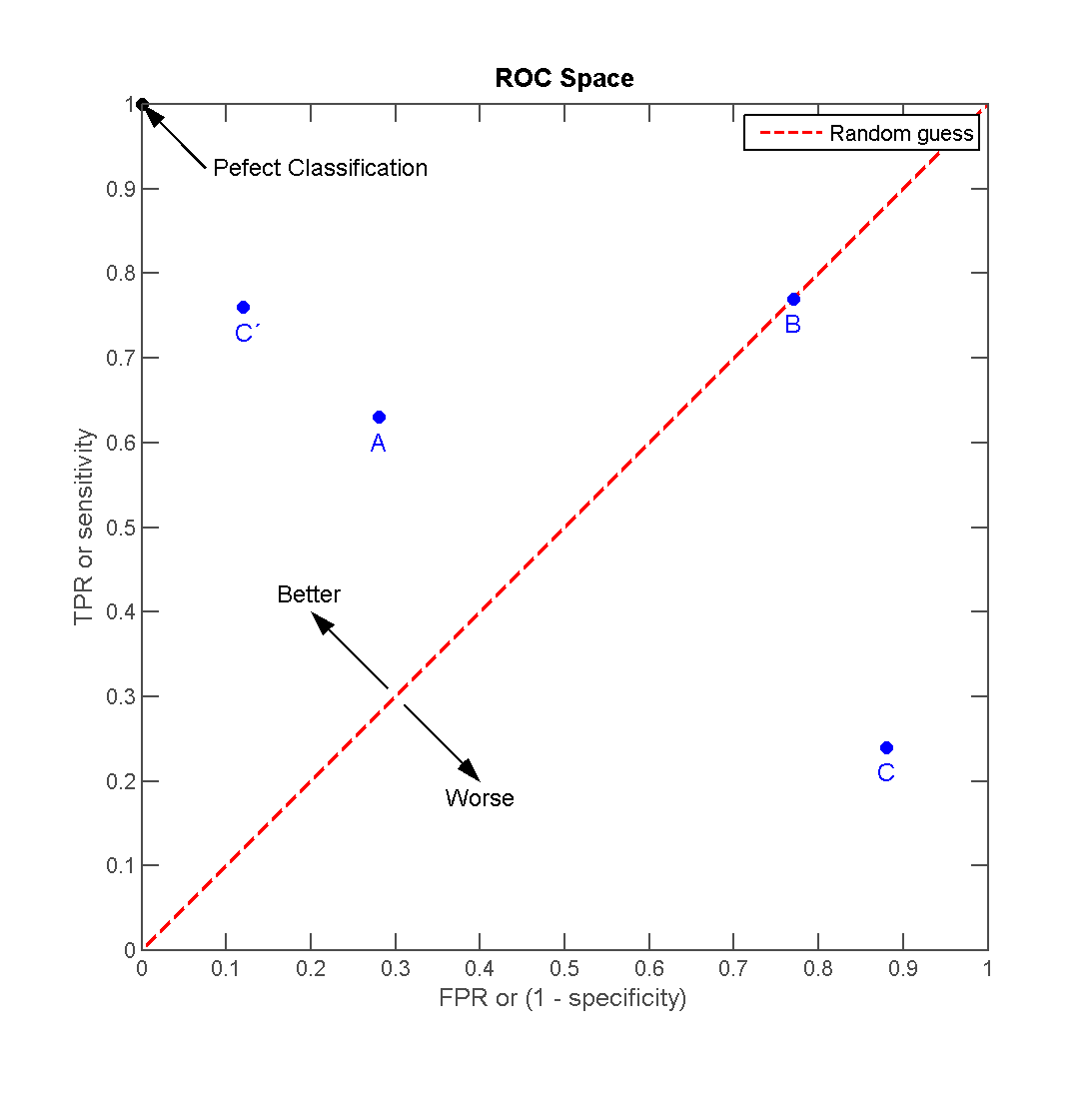
Looking at the axes on our great big graph:
- The X axis is the “false positive rate” (FPR) - the number of false positives (you labeled the GOOD but they’re actually BAD) divided by the number of actual BAD instances
- the Y axis is the “true positive rate” (TPR) - the number of true positives (labeled GOOD and actually GOOD) divided by the number of actual GOOD instances
The intuition here is that these are conflicting measurements: the more you
make your model work to detect GOOD instances (higher true positive rate), the
more false positives you end up catching in your net (the false positive rate).
The legal axiom “innocent until proven guilty” is a great example of a policy
designed to drive down the false positive rate (where positive means a guilty
verdict in a court of law). As pointed out ad nauseum by seemingly thousands
of American legal dramas, this also leads to a lower true positive rate (guilty
people going free). The other end of the spectrum is the scumbag
evil spam purveyor. A spammer classifies every potential email
address as a positive, where positive means a human who read and respond to the
email by purchasing something. If you’re spamming a bazillion people, a true
positive rate of even 0.001% results in financial gain. 1
Let’s take some easy example models and some concrete numbers:
- Jerk Pessimist Model – If your model always guesses BAD, then you have no positives. Your TPR and FPR are both 0 and your model is a point at (0,0) on the graph
- Silly Optimist Model – If your model always guesses “GOOD”, then everything is a positive. In this case your model is a point at (1,1) at the top right
- Coin Flipper – If you model randomly flips a coin to decide, both rates will be 0.5 (50-50) and therefore smack in the middle of the graph.
So let’s get the guessing out of the way: if you change the probability of guessing from a coin, that will move your model up or down that diagonal red line in the graph. We want to be above that line.
The next thing to realize is that we don’t want to find a single point for your model. We want to see all the points your model can occupy. Luckily, most classification models don’t give a thumbs up or thumbs down: they usually give a score from 0.0 – 1.0 where 0.5 is “shrug”, 0.0 is 100% BAD, and 1.0 is 100% sure that it’s GOOD. Models meant for multi-label classification might give a single 0-1 score for every possible label, but in our simple binary instance the score for BAD would be 1-GOOD.
the more you make your model work to detect GOOD instances (higher true positive rate), the more false positives you end up catching in your net (the false positive rate)
That setup gives us a final dial to turn. Once we have a model spitting out GOOD scores, we can choose what threshold we want to use to actually predict a label. As our threshold goes up, we drive down the false positive rate, but we’ll also miss some true positives. If we move the threshold down, our true positive rate will go up but we’ll inevitably get false positives. Depending on what you’re trying to do (and the cost of a false positive), you will choose different settings for that dial. Who cares about false positives for a coupon-mailing algorithm? But if your death robot is about to open fire on an intruder, you better be sure.

Regardless, all those possible points form a curve. AUC is Area Under that Curve. It’s a straight Calc I (or is it Calc II?) integral, although it’s estimated empirically.
Back to our examples:
- Our coin flipper models have an AUC of 0.50
- If you had a magically perfect algorithm that was always right, it’s AUC would be 1.0
- Lots of medical people want an AUC of 0.99 or better for some applications
- For a lot of applications, an AUC of 0.75 or better would have people dancing in the streets
It all depends on what you’re trying to do.
Who cares about false positives for a coupon-mailing algorithm? But if your death robot is about to open fire on an intruder, you better be sure.
There are some nice advantages to AUC. Namely:
- People want to report accuracy, but they frequently mean TPR. Sometimes that’s fine, but it’s seldom the whole picture
- Lots of training and scoring algorithms assume that the classes are balanced (in our case that means that we would have about 50% GOOD and 50% BAD in both our training and testing sets). AUC doesn’t have this requirement, which makes it an especially nice metric for unbalanced data sets (like most medical detection applications)
So let’s day you don’t have much domain knowledge about that data you’ve been handed. It’s a bunch of flibberty-gibbit data, and you’re supposed to build a model to discriminate between the wo-wo and ya-ya classes. You build a model and get an AUC score of 0.73. What does than even mean? Keep in mind that often the best way to look at AUC is as a relative score. If there’s an existing model (or this is a Kaggle contest), the real question is where your 0.73 lands with other models/competitors. It’s a good way to compare model performance for classification. This might also be a good time to create some “baseline” models to see how your hard work compares with the simplest (silliest) models possible. When there’s a binary classification task like our fictional flibberty-gibbit dataset, a good starting set of baselines would be:
- “Constant” model that always outputs “wo-wo”
- “Constant” model that always outputs “ya-ya”
- “Random” model that always classifies based on a coin toss (where the probability is based on the frequency of each class).
If your model’s AUC score is right in there with these baselines, then your model, your data, or your evaluation criteria is broken. In case you’re wondering, it’s no coincidence that these were the “easy example models” above. As silly as these models might seem, they can give you a good idea of the bare minimum that any model should accomplish.
Pretty easy right? The number we’ve been calling “AUC” is also known as the “AUC Score”. So now you’re probably wondering “what’s with all this ROC business?”
Well, our AUC score is the area under a curve. That curve is named… wait for it… the “Receiver Operating Characteristic Curve”, aka ROC or ROC Curve.
Go forth and classify!
References
Links used in this article (or that you might want to check out):
- Kaggle: https://www.kaggle.com
- Receiver Operating Characteristic on Wikipedia: https://en.wikipedia.org/wiki/Receiver_operating_characteristic